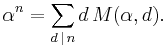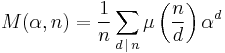Necklace polynomial

In combinatorial mathematics, the necklace polynomials, or (Moreau's) necklace-counting function are the polynomials $M (α, n)$ in α such that

$\alpha^n = \sum_{d\,|\,n} d \, M(\alpha, d).$

By Möbius inversion they are given by

$M(\alpha,n) = {1\over n}\sum_{d\,|\,n}\mu\left({n \over d}\right)\alpha^d$

where $μ$ is the classic Möbius function.

The necklace polynomials are closely related to the functions studied by C. Moreau (1872), though they are not quite the same: Moreau counted the number of necklaces, while necklace polynomials count the number of aperiodic necklaces.

The necklace polynomials appear as:

the number of aperiodic necklaces (also called Lyndon words) that can be made by arranging $n$ beads the color of each of which is chosen from a list of $α$ colors (One respect in which the word "necklace" may be misleading is that if one picks such a necklace up off the table and turns it over, thus reversing the roles of clockwise and counterclockwise, one gets a different necklace, counted separately, unless the necklace is symmetric under such reflections.);
the dimension of the degree $n$ piece of the free Lie algebra on $α$ generators
the number of monic irreducible polynomials of degree $n$ over a finite field with $α$ elements (when $α$ is a prime power).
the exponent in the cyclotomic identity.
The number of Lyndon words of length n in an alphabet of size α.

Values

$M (α,1) = α$
$M (α,2) = (α 2 - α)/2$
$M (α,3) = (α 3 - α)/3$
$M (α,4) = (α 4 - α 2)/4$
$M (α,5) = (α 5 - α)/5$
$M (α,6) = (α 6 - α 3 - α 2 + α)/6$
$M (α, p n) = (α p n - α p n - 1)/ p n$ for $p$ prime
$\displaystyle M(\alpha\beta, n)=\sum_{[i,j]=n}(i,j)M(\alpha,i)M(\beta,j)$ where (i,j) is the highest common factor of i and j and [i,j] is their least common multiple.

References

Moreau, C. (1872), "Sur les permutations circulaires distinctes (On distinct circular permutations)" (in French), Nouvelles annales de mathématiques, journal des candidats aux écoles polytechnique et normale, Sér. 2 11: 309–314, JFM 04.0086.01, http://www.numdam.org/item?id=NAM_1872_2_11__309_0
Metropolis, N.; Rota, Gian-Carlo (1983), "Witt vectors and the algebra of necklaces", Advances in Mathematics 50 (2): 95–125, doi:10.1016/0001-8708(83)90035-X, ISSN 0001-8708, MR 723197

Necklace polynomial

Values

See also

References